Euler's theory of columns

Columns and Struts:

• A structural member subjected to an axial compressive force is called strut. As per definition strut may be horizontal, inclined or even vertical.
• The vertical strut is called a column.

Euler’s Column Theory

Assumptions of Euler's theory:

Euler's theory is based on the following assumptions:

(i). Axis of the column is perfectly straight when unloaded.

(ii). The line of thrust coincides exactly with the unstrained axis of the column.

(iii). Flexural rigidity El is uniform.

(iv) Material is isotropic and homogeneous.

 

Limitation of Euler’s Formula

• There is always crookedness in the column and the load may not be exactly axial.
• This formula does not take into account the axial stress and the buckling load is given by this formula may be much more than the actual buckling load.

Euler’s Buckling (or crippling load)

• The maximum load at which the column tends to have lateral displacement or tends to buckle is known as buckling or crippling load. Load columns can be analysed with the Euler’s column formulas can be given as  

  

where, E = Modulus of elasticity, L_e= Effective Length of column, and I = Moment of inertia of column section.

  For both end hinged:

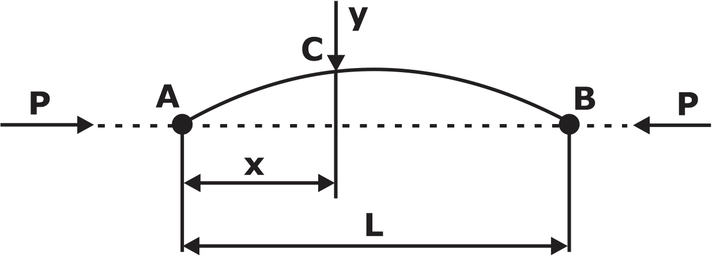
in case of Column hinged at both end L_e = L

 

 For one end fixed and other free:

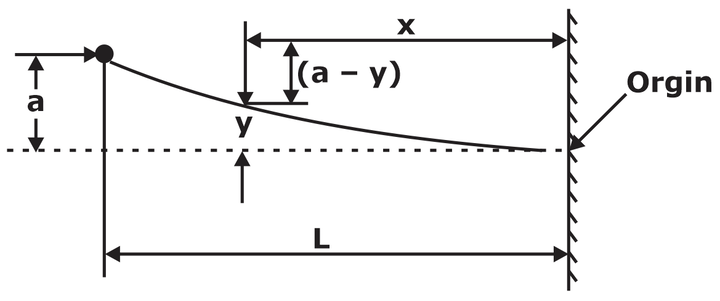
in case of column one end fixed and other free: L_e = 2L

 For both end fixed:

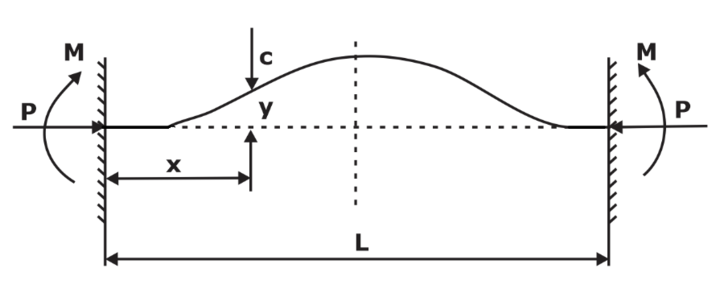
in case of Column with both end Fixed L_e = L/2

For one end fixed and other hinged:

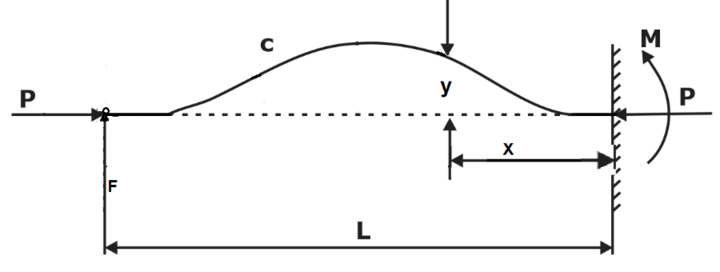
in case of Column with one end fixed and other hinged L_e = L/√2

Effective Length for different End conditions

Slenderness Ratio ( S)

The slenderness ratio of a compression member is defined as the ratio of its effective length to least radius of gyration.

 

Modes of failure of Columns

 Rankine’s Formula:

Rankine proposed an empirical formula for columns which coven all Lasts ranging from very short to very long struts. He proposed the relation

   P_c = σ_C. A = ultimate load for a strut

Eulerian crippling load for the standard case