generation & change in entropy

Entropy

The Clausius Inequality

• The first law is just a balance of energy.
• The second law states an inequality ie an irreversible process is less efficient than a reversible process.
• One of such important inequalities is that of the Clausius inequality in Thermodynamics according to which the cyclic integral of δQ / T is always less than or equal to zero.
• It is valid for all cycles, be it reversible or irreversible.
• The basis for the definition of a new property called entropy is formed by the Clausius inequality.

• For an internally reversible process, the cyclic integral of δQ / T is zero.
• If the cyclic integral of a quantity is zero, it means that it depends on the state only and not the process path. Hence, it is a property.
• For an irreversible process, the value of entropy change for a closed system is greater than the value of integral of dQ/T evaluated for that process.
• If the energy exchange takes place, δQ will be the energy transfer from the surroundings to the system.

 

 

 

 

 

 

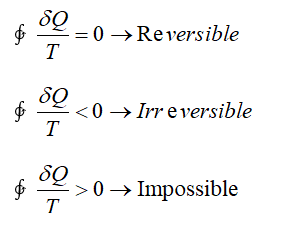
TEMPERATURE-ENTROPY PLOT

Now dQ_rev, = TdS

Thus, area under the T -S plot on S axis will give the heat transfer in a reversible process.

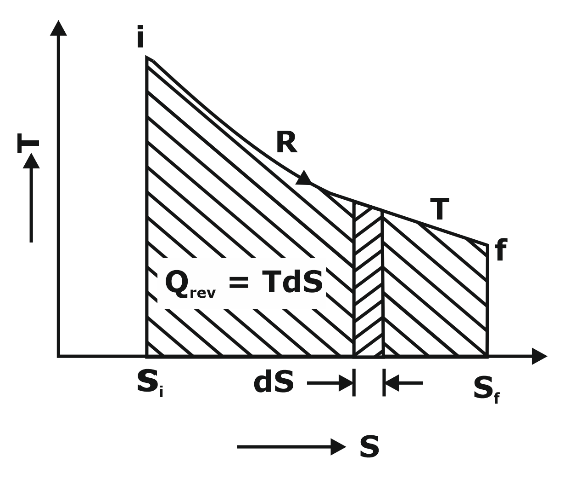
Fig.: Area under a reversible path on the T-s plot

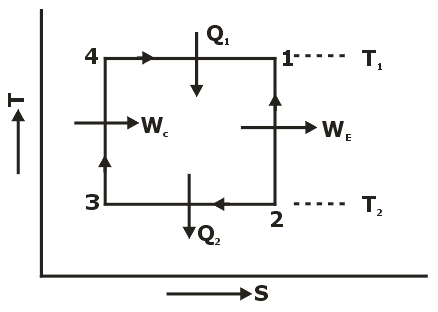
CARNOT CYCLE

The Carnot cycle comprises of two reversible isotherms and two reversible adiabatic processes, forms a rectangle in the T-S plane.

process 1 – 2: The reversible adiabatic expansion of the system developing W_E amount of work.

process 2 – 3: The reversible isothermal heat rejection from the system to the external sink at temperature T_2.

process 3 – 4: The reversible adiabatic compression of the system absorbing W_c amount of work.

Process 4 – 1: The reversible isothermal heat addition Q₁ to the system at temperature T₁ from an external source.

THE INCREASE OF ENTROPY PRINCIPLE:

Let us assume a cycle that is made up of two processes as shown below:

process 1-2, which is an arbitrary process (reversible or irreversible),

and process 2-1, which is internally reversible in nature, as shown in the Figure below,

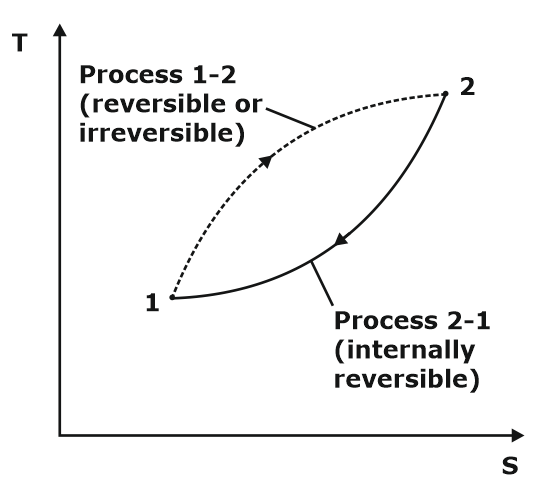
Fig.: Combination of reversible & irreversible process

where the equality is for the internally reversible process and the inequality for the irreversible process.

It should be kept in mind that the entropy generation S_gen is always a positive quantity or zero. Its value is process dependent, and thus it is not a property of the system.

For an isolated system, 

dQ = 0 since no energy interaction occurs between the system and the surrounding.

Therefore, for an isolated system

dS_iso ≥ 0

For a reversible process,

 dS_iso = 0

implies,  S = constant

 For an irreversible process

dS_iso > 0

Entropy change of the system:

Entropy charge of the system is summation entropy change due to internal irreversibility and entropy change due to external interaction

dS = (dS)_Irr, + (dS)_EI

 

 T-dS EQUATION

........(1)

........(2)

Note:

Equation (1) & (2) are applicable for both reversible process as well as the irreversible process because it contents all properties.

APPLICATIONS OF ENTROPY PRINCIPLE:

For every irreversible process, there is an increase of entropy of the universe, and this entropy increase determines the extent of irreversibility of the process. The higher the entropy increase of the universe; the higher will be the irreversibility of the process.

Some of the applications of the entropy principle are illustrated in the following.

(A) Heat transfer through a Finite Temperature Difference.

(B) Two fluids mixing with each other.

(C) Maximum Work that can be obtained from Two Finite Bodies at Temperatures T₁ and T₂ interacting in a reversible manner.