heat transfer through fins

Heat Transfer from Extended Surface (Fin):

• A fin is a surface that extends from an object to increase the rate of heat transfer to or from the environment by increase convection.
• Adding a fin to an object increases the surface area and can sometimes be an economical solution to heat transfer problems.
• Finned surfaces are commonly used in practice to enhance heat transfer. In the analysis of the fins, we consider steady operation with no heat generation in the fin.
• We also assume that the convection heat transfer coefficient h to be constant and uniform over the entire surface of the fin.

• The rate of heat transfer from a solid surface to atmosphere is given by Q = hA ∆ T where, h and ∆T are not controllable.
• So, to increase the value of Q surface area should be increased. The extended surface which increases the rate of heat transfer is known as fin.

 Generalized Equation for Fin Rectangular fin:

Where A_c and A_s are cross-sectional and surface area:

And θ(x)=t(x)–t_a

Heat balance equation if A_c constant and A_s ∞ P(x) linear:

• General equation of 2^nd order: θ = c₁e^mx + c₂e^–mx
• Heat dissipation can take place on the basis of three cases.

Case 1: Heat Dissipation from an Infinitely Long Fin (l → ∞):

• In such a case, the temperature at the end of Fin approaches to surrounding fluid temperature ta as shown in figure. The boundary conditions are given below
• At x=0, t=t₀ : θ = t₀ – t_a = θ₀
• At x =L→ ∞: t = t_a, θ = 0
  
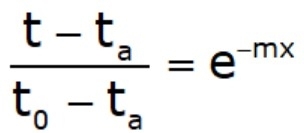
  θ = θ₀ e^–mx

• Heat transfer by conduction at base:
  

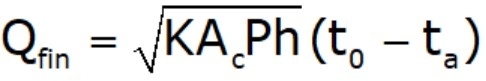
Case 2: Heat Dissipation from a Fin Insulated at the End Tip:

• Practically, the heat loss from the long and thin film tip is negligible, thus the end of the tip can be, considered as insulated.
• At x=0, t=t₀ and θ = t₀ – t_a = θ₀
  at 
  
  
  

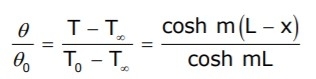
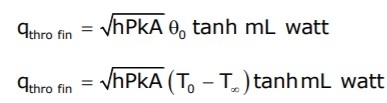
Case 3: Heat Dissipation from a Fin loosing Heat at the End Tip:

• The boundary conditions are given below.
• At x=0, t = t₀ and θ = θ₀
• At x=l
  Q_conduction = Q_convection

        

Fin Efficiency:

Fin efficiency is given by:

• If l → ∞ (infinite length of fin):
  
  
• If fin is with insulated tip:
   

• If finite length of fin:
  
  

Note: The following must be noted for a proper fin selection:  

• The longer the fin, the larger the heat transfer area and thus the higher the rate of heat transfer from the fin.
• The larger the fin, the bigger the mass, the higher the price, and larger the fluid friction.
• The fin efficiency decreases with increasing fin length because of the decrease in fin temperature with length.

Fin Effectiveness: 

• The performance of fins is judged on the basis of the enhancement in heat transfer relative to the no‐fin case, and expressed in terms of the fin effectiveness: 
  
  
• For a sufficiently long fin of uniform cross‐section Ac, the temperature at the tip of the fin will approach the environment temperature, T_∞. By writing energy balance and solving  the differential equation, one finds:
  
  
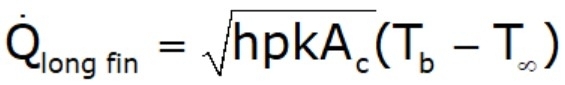
  where A_c is the cross‐sectional area, x is the distance from the base, and p is perimeter.  The effectiveness becomes: 
  

To increase fins effectiveness, one can conclude:  

• The thermal conductivity of the fin material must be as high as possible     
• The ratio of perimeter to the cross‐sectional area p/Ac should be as high as possible 
• The use of fin is most effective in applications that involve low convection heat transfer coefficient, i.e. natural convection.