thermodynamic relations

 INTRODUCTION

The properties such as temperature pressure, volume and mass can be calculated directly.

The substances properties such as density (ρ) and specific volume(v) can be estimated using some simple relations.

However energy, enthalpy (h) and entropy (s) are not very easy to determine because they are not measurable or can not be easily expressed in terms of measurable properties through some simple relations.

1. Maxwell’s Equations

These are the set of equations that establish the relation between the partial derivatives of properties P, V, T, and S of a simple compressible system.

dU = TdS – PdV

dH = TdS + VdP

Helmholtz function

F = U – TS (availability of closed system)

Gibb’s function

G = H – TS (availability of open system)

For all real processes, the value of the Helmholtz function & Gibbs function decreases & attains a min value at equilibrium.

Helmholtz function

F = U – TS (availability of closed system)

Gibb’s function

G = H – TS (availability of open system)

For all real processes the value of Helmholtz function & Gibbs function decreases & attains a min value at equilibrium.

Hence Four Maxwell’s relations are,

COEFFICIENT OF VOLUME EXPANSION (β)

It is rate of change of volume with respect to temperature at constant pressure.

ISOTHERMAL COMPRESSIBILITY (K_T)

It shows the rate of change of volume with respect to pressure at a constant temperature or at isothermal conditions.

2. T-dS Equation

 

This is known as the first Tds equation

This is known as the second TdS equation.

T = Positive

C_p –C_v = +ve

C_p > C_v

_{3. Energy Equation}

Joule Thompson Coefficient (µ)

When a fluid passes through the porous plug, capillary tube, or valve, its pressure decreases. The throttling process is isenthalpic in nature. The temperature behavior of the fluid during throttling is described by the joule Thompson coefficient(µ),

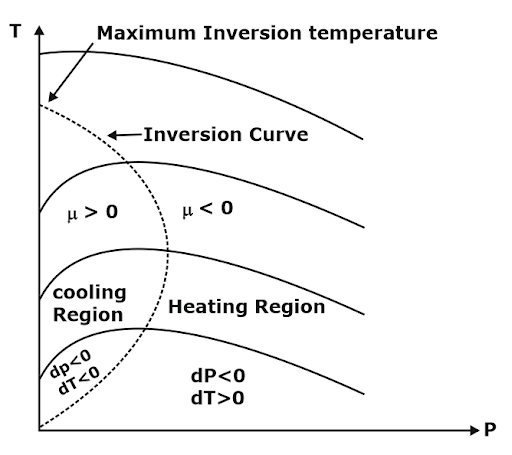
                     Fig:1

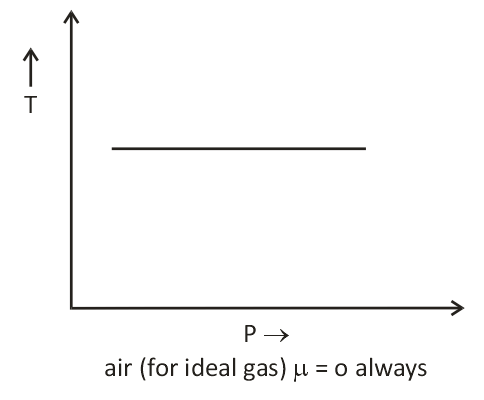
                   Fig:2

Important points:

1. Joule Thomson coefficient is +ve in cooling region i.e slope of isenthalpic curve on T – P diagram is +ve in cooling region,
2. μ is –ve in heating region i.e the slope of isenthalpic curve on T – P diagram is –ve in the heating region,
3. There is nothing as a heating or cooling region for an ideal gas & the value of the joule Thomson coefficient is zero everywhere.

 4. Clausius Clapeyron Equations

Clausius Clapeyron equations is a relationship between saturation pressure, temperature, and enthalpy of vaporization and the specific volume of two phases involved. This equation helps in calculations of properties in two-phase regions.

 

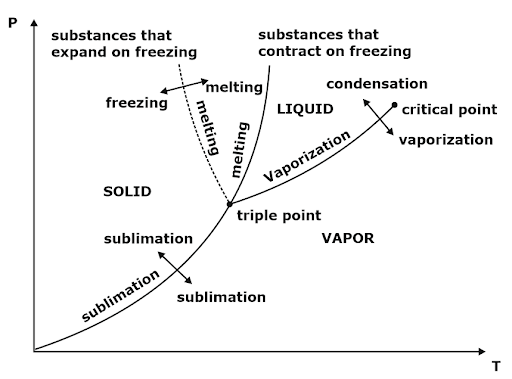
                                Fig:3

The above equation is called the Clausius Clapeyron equation. It helps to determine enthalpy change associated with phase change by measuring pressure, temperature, and volume.